There’s something profoundly unsettling about discovering that the universe seems to have a favorite number. Not unsettling in a frightening way, but in the way that makes you pause and wonder whether we're looking at coincidence or catching glimpses of something deeper—a kind of cosmic DNA that threads through everything from the spiral of your morning coffee to the arms of distant galaxies. As astrophysicist Neil deGrasse Tyson reminds us, “The universe is under no obligation to make sense to you.” And yet, we find that it speaks to us in the language of mathematics.
And at the heart of it all is a number: φ (phi), the Golden Ratio, approximately 1.618. It doesn’t travel alone, either. It brings with it the Fibonacci sequence and Lucas numbers, a mathematical trinity that appears to be woven into the very fabric of reality with a persistence that borders on the mystical.
The Golden Ratio: Mathematics with Attitude
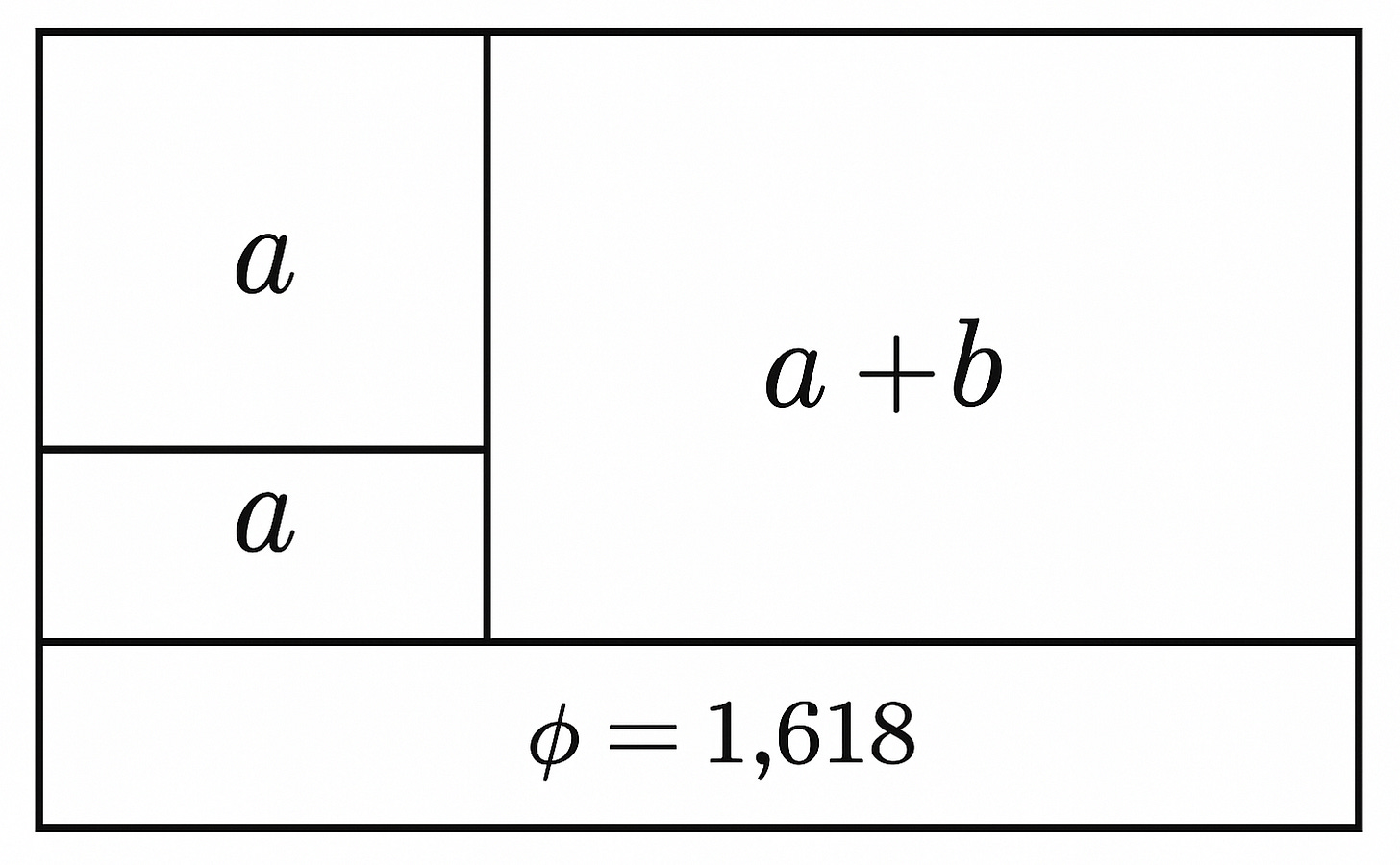
Let's start with φ itself. Picture this: you're tasked with dividing a line segment in the most aesthetically pleasing way possible. Not in half—that’s too obvious, too symmetrical. Instead, you want to create a division that feels naturally balanced, where the relationship between the parts creates a sense of harmony that your eye can't quite explain but definitely feels.
You'd end up dividing it so that the ratio of the whole line to the longer segment equals the ratio of the longer segment to the shorter one. What's remarkable is that this seemingly arbitrary aesthetic choice leads us to a number that solves the elegant equation . Think about that for a moment. We have a number that, when squared, equals itself plus one. It's the only positive number with this property, and it emerges not from abstract mathematical manipulation but from our intuitive sense of what looks "right."
The ancient Greeks knew this. Around 300 BCE, Euclid of Alexandria—the father of geometry whose Elements would become one of the most influential textbooks in history—called it the "extreme and mean ratio." Euclid was a systematic thinker who transformed scattered geometric knowledge into a coherent logical framework, though he probably had no idea he was describing what would later be found spiraling through sunflower heads and hurricane formations.
More than a thousand years later, Luca Pacioli (1447-1517), a Franciscan friar and close friend of Leonardo da Vinci, encountered Euclid's work and was utterly captivated. Writing in 1509, Pacioli called it "divine proportion"—a mathematical expression of God's sense of design. His book De Divina Proportione, illustrated by Leonardo himself, spread the concept throughout Renaissance Europe and cemented the idea that mathematics could reveal divine beauty in nature.
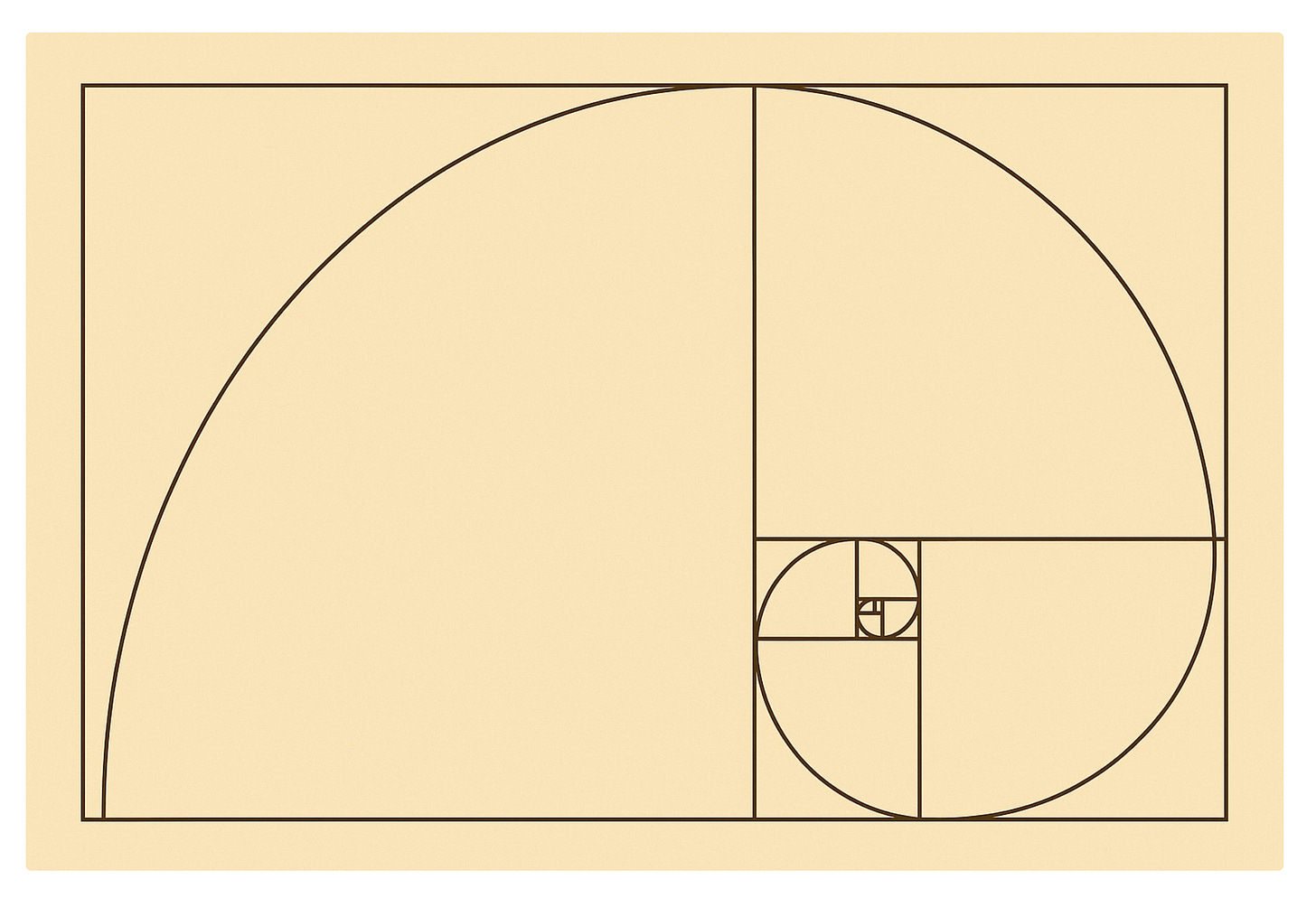
Here's where it gets interesting. Take a Golden Rectangle—one whose sides are in the ratio φ:1. Remove a square from it, and the remaining rectangle has exactly the same proportions as the original. Do it again. And again. Each time, you're left with a perfect replica of what you started with, just smaller.
Connect the corners of these nested squares with a smooth curve, and you get the Golden Spiral—a shape that will haunt you once you start seeing it everywhere.
The Fibonacci Sequence: Nature's Accountant
Now meet the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... Each number is simply the sum of the two before it. Leonardo Fibonacci (c. 1170-1250), born Leonardo Pisano, introduced this sequence to Europe in 1202 through his revolutionary book Liber Abaci (The Book of Calculation).
Fibonacci was a merchant's son who traveled extensively throughout the Mediterranean, where he encountered the Hindu-Arabic numeral system that we use today. His book wasn't just about rabbit breeding problems—it was a mathematical revolution that introduced Europeans to the concept of zero, algebraic methods, and efficient calculation techniques that would transform commerce and science. The sequence that bears his name was actually just a small example in a much larger work, initially posed as a theoretical problem about rabbit breeding: "How many pairs of rabbits can be produced from a single pair in a year if each pair bears a new pair every month, and each new pair becomes fertile after one month?"
What Fibonacci couldn't have known was that he was describing nature's preferred counting system, a pattern that would be recognized centuries later as fundamental to biological growth and form. His work built directly on the mathematical foundations laid by Euclid, using geometric principles to explore numerical relationships.
Walk through any garden, and you're walking through a Fibonacci exhibition. Those daisies scattered across the lawn? Count their petals. You'll find 13, 21, 34, or 55 petals far more often than any other number. Lilies stubbornly stick to 3 petals, buttercups to 5—all Fibonacci numbers. It's as if someone handed nature a cheat sheet.
But the real showstopper is the sunflower. Look at the center of a mature sunflower head, and you'll see two families of spirals winding in opposite directions. Count them. In one direction, you might find 34 spirals; in the other, 55. Sometimes it's 55 and 89, or even 89 and 144. Always consecutive Fibonacci numbers, never exceptions. This isn't coincidence—it's optimization. Plants that arrange their seeds according to Fibonacci numbers pack them most efficiently, maximizing their reproductive success.
Lucas Numbers: The Overlooked Sibling
Lucas numbers: 2, 1, 3, 4, 7, 11, 18, 29—follow the same addition rule as Fibonacci numbers but start with different initial conditions. Named after François Édouard Anatole Lucas (1842-1891), a French mathematician who was fascinated by number theory and recreational mathematics, they're like Fibonacci's mathematical twin, sharing the same DNA but expressing it differently.
Lucas was a contemporary of other great French mathematicians like Henri Poincaré and worked at the École Polytechnique. He's perhaps best known for proving that the Mersenne number was prime—a calculation he performed by hand in 1876, long before computers existed. But his investigation of what he called "secondary sequences" related to Fibonacci numbers revealed deep connections that Fibonacci himself never explored.
Interestingly, Lucas was among the first to recognize that the ratio of consecutive Fibonacci numbers converged to the Golden Ratio—a connection that neither Euclid nor Fibonacci had explicitly noted. His work represented a bridging of ancient geometric insights with modern number theory, showing how mathematical ideas separated by millennia could illuminate each other in unexpected ways.
What's fascinating is that Lucas numbers converge to φ just as readily as Fibonacci numbers do. Divide any Lucas number by its predecessor, and as the numbers get larger, you approach φ with the same relentless precision. It's as if nature has multiple pathways to the same fundamental truth.
The Deep Connections: Where Mathematics Becomes Poetry
Here's where these three concepts stop being separate ideas and start being facets of something larger. Take any Fibonacci number and divide it by the one before it: 89 ÷ 55 = 1.618..., 144 ÷ 89 = 1.617..., 233 ÷ 144 = 1.6180... Each division gets you closer to φ. The same thing happens with Lucas numbers. It's as if both sequences are racing toward φ from different starting points but along parallel tracks.
This convergence isn't just mathematically elegant—it's practically useful. When engineers need to search through large datasets, they often use Fibonacci search algorithms because the Golden Ratio provides optimal efficiency. When artists want to create pleasing compositions, they intuitively gravitate toward proportions that echo φ.
But the deeper you dig, the stranger it gets. In matrix mathematics, the fundamental properties of Fibonacci and Lucas numbers emerge from the eigenvalues of simple 2×2 matrices.
In continued fractions, φ has the simplest possible representation: 1 + 1/(1 + 1/(1 + 1/...)). It's the most irrational of all irrational numbers, meaning it's the hardest to approximate with simple fractions—a property that, as we'll see, has profound consequences for planetary stability.
The Mathematical Underpinnings of Physics
The influence of these topics—the Golden Ratio (φ), the Fibonacci sequence, and related concepts—on our understanding of physics is profound, suggesting that mathematics isn't merely a descriptive tool but an integral part of the universe's operational code. These numerical patterns appear at scales ranging from the quantum to the cosmic, hinting at a deep, elegant simplicity beneath apparent complexity.
Quantum Mechanics and Quasicrystals
In the strange world of quantum mechanics, where particles exist in a state of probability, φ and Fibonacci numbers emerge in the study of particle behavior. For instance, some researchers have found that these numbers govern the energy levels of certain atomic systems. One of the most fascinating appearances is in quasicrystals, a state of matter with an ordered but non-repeating structure. Unlike regular crystals, whose atoms are arranged in a repeating pattern, quasicrystals are aperiodic. The geometry of their atomic lattice, first discovered in the 1980s, is often based on φ, leading to structures with a five-fold symmetry that was once considered impossible. This discovery earned its founder, Dan Shechtman, a Nobel Prize in Chemistry and fundamentally changed our understanding of solid matter.
Black Holes and Cosmic Stability
At the cosmic scale, the Golden Ratio marks critical transition points in the dynamics of black holes. The ratio of a black hole’s mass to its charge determines its thermodynamic properties. When this ratio equals φ, the black hole's specific heat changes from positive to negative, marking a boundary between stable and unstable states. This is not a coincidence but a consequence of the underlying mathematical principles that govern gravity and thermodynamics. Kip Thorne is a Nobel Prize–winning physicist from Caltech, he said “Black holes are not the monsters we once imagined. Their stability, the way they sit at the crossroads of gravity, quantum mechanics, and thermodynamics, makes them the most natural laboratories in the universe.”
Furthermore, the Kolmogorov-Arnold-Moser (KAM) theorem in classical mechanics reveals φ's role in ensuring the long-term stability of planetary systems. The theorem shows that orbits are most stable when their periods are related by the "most irrational" numbers—and φ holds this title. This property, known as a Diophantine condition, prevents tiny gravitational perturbations from building up over time and destabilizing the system. It suggests that our solar system, which has remained stable for billions of years, may have endured because the orbital periods of its planets are subtly related by irrational numbers that resist resonance. In this view, φ isn't just a beautiful number; it's a cosmic shock absorber that keeps planets from careening into their suns.
From Micro to Macro
The consistency with which these numbers appear across different physical domains—from the microscopic arrangement of atoms in quasicrystals to the macroscopic stability of galaxies and planetary orbits—suggests a unified mathematical language for the universe. It challenges the traditional view of mathematics as a human invention used to describe nature and instead points to the possibility that mathematics is a fundamental discovery, the very blueprint of reality. This has profound implications for theoretical physics, as it encourages scientists to look for mathematical elegance and symmetry as guiding principles in the search for a unified theory of everything. The Golden Ratio, in this sense, becomes a crucial piece of the puzzle, a number that connects the aesthetics of art with the fundamental laws of physics.
Art and Architecture: The Aesthetics of Mathematics
Humans seem to have an innate appreciation for φ proportions, even when we're not consciously aware of them. Salvador Dalí (1904-1989), the surrealist master, was obsessed with the Golden Ratio, using it explicitly in "The Sacrament of the Last Supper," where he painted the scene inside a perfect Golden Rectangle and placed a dodecahedron—a geometric form whose proportions are entirely determined by φ—at the center. Dalí's mathematical interests weren't superficial; he collaborated with mathematicians and scientists throughout his career, seeing mathematics as a bridge between the rational and the mystical. As art historian Martin Kemp has noted, for Dalí, the Golden Ratio was not merely an aesthetic tool but a symbol of his attempt to bridge the spiritual with the scientific.
Of course, no discussion of this topic would be complete without Leonardo da Vinci (1452-1519), who had an insatiable curiosity for both art and science. His close friendship with the mathematician Luca Pacioli, who called the Golden Ratio "divine proportion," deeply influenced his work. Leonardo's famous drawing, Vitruvian Man, is a testament to this fusion of art and mathematical principles. The work meticulously combines the ideal human form with geometric shapes, showing a man inscribed within a circle and a square, echoing the ancient Roman architect Vitruvius’s belief that the human body's proportions were a key to understanding the natural order of the universe.
While Leonardo's direct use of the Golden Ratio in his paintings is a subject of scholarly debate, its presence in some of his most celebrated works, like the Mona Lisa, has been widely studied.
Some analysts claim that the proportions of the painting's composition, the sitter's face, and even the placement of her hands and eyes align with the Golden Ratio.
Whether Leonardo intentionally used this ratio or simply had an intuitive artistic sense that gravitated toward these harmonious proportions remains a fascinating mystery. The debate, however, highlights a fundamental point: great art often achieves a timeless, universal appeal by reflecting principles of harmony and balance that are also found in mathematics and nature.
Another visionary who embraced this philosophy was the architect Frank Lloyd Wright (1867-1959). As a leader of the Prairie School movement, he rejected the rigid, classical styles of the past and sought to create a new, distinctly American architecture that was in harmony with its environment. Wright’s designs, from his iconic Fallingwater to the Solomon R. Guggenheim Museum, were deeply influenced by a philosophy of organic architecture, which held that buildings should grow from their surroundings just as a flower or tree does.
To achieve his philosophy of organic architecture, he frequently employed natural, geometric progressions, including Fibonacci sequences and Golden Ratio proportions, in his floor plans, facades, and even in the decorative motifs of his stained glass and furniture. By integrating these mathematical patterns, Wright created spaces that felt both natural and meticulously designed, bridging the gap between human creation and the inherent order of the natural world.
The connection between mathematics and aesthetics wasn't new—it traced back through Pacioli and Leonardo's collaboration, through the Islamic geometric traditions that influenced Fibonacci's mathematical education, and ultimately to the Greeks who first codified these relationships. What was new was the systematic application of these ancient insights to modern design and architecture. The dimensions of the Parthenon have been the subject of long-standing debate, with some scholars arguing they were deliberately proportioned according to the Golden Ratio, while others contend this is a retrospective interpretation.
But here's what's truly intriguing: studies suggest that people find Golden Rectangle proportions more pleasing than other rectangles, even when they have no idea what they're looking at. Show someone a series of rectangles with different proportions, and they'll consistently rate those closest to the Golden Rectangle as most attractive. It's as if φ is hardwired into our aesthetic sense.
The Golden Ratio in Musical Composition
The influence of the Golden Ratio and the Fibonacci sequence isn't limited to the visual arts and natural sciences; it extends into the world of music, a realm of sound, rhythm, and harmony. While the connections here are often debated and less concrete than in botany or physics, many composers, from classical masters to modern innovators, have consciously or unconsciously incorporated these mathematical principles into their work.
The core idea is that the same proportions found to be aesthetically pleasing in a painting, or a seashell might also create a sense of balance and harmony in a musical piece.
A musical composition can be broken down into sections—movements, themes, verses, or even individual measures. Composers have used the Golden Ratio to determine the placement of key events within a piece's total length, such as a climax, a significant theme, or a major change in tempo. The theory is that placing these pivotal moments at a point that divides the whole into a Golden Ratio makes the composition feel naturally balanced and complete to the listener.
Classical and Modern Composers
Béla Bartók (1881-1945): The Hungarian composer Béla Bartók is one of the most well-documented examples of a composer who intentionally used Fibonacci numbers and the Golden Ratio. He based the structure and timing of many of his compositions on these principles. For example, in his Music for Strings, Percussion and Celesta, the form is a tightly constructed arch. The number of bars in each section often corresponds to Fibonacci numbers, with the climax of the piece placed exactly at the Golden Ratio point. The number of notes in chords and the length of musical phrases in his work also frequently follow these numerical patterns.
Claude Debussy (1862-1918): While less explicit than Bartók, some musicologists have argued that the Impressionist composer Debussy used the Golden Ratio in his pieces to create his signature sense of ethereal harmony and fluidity. The structure of works like his piano piece Reflets dans l'eau has been analyzed to show that its major musical phrases and climax points align with the Golden Ratio, creating a sense of natural, unfolding beauty.
Iannis Xenakis (1922-2001): The Greek-French composer and architect Iannis Xenakis took the connection between mathematics and music to a new level. He saw music not as a linear progression but as a sonic architecture, using mathematical models, including probability theory and game theory, to generate his compositions. While his work isn't always directly tied to the Golden Ratio, his entire philosophy was built on the idea that deep mathematical structures could be used to create complex, compelling, and surprising sounds.
Why It Works
The influence of these mathematical concepts on music is more than just a historical curiosity. It reflects a deeper connection between the human brain and patterns. Our minds are naturally wired to seek out order and recognize patterns, even subconsciously. The Golden Ratio, being the "most irrational" number, avoids simple, predictable subdivisions (like halves or quarters) while still providing a sense of proportion and balance. This creates a composition that feels organized and satisfying without being boring or overly symmetrical. It's a sweet spot between complete chaos and rigid predictability, which our brains find both engaging and aesthetically pleasing.
Nature's Efficiency Engine
But why does nature favor these patterns? The answer lies in efficiency and optimization. When a sunflower arranges its seeds in Fibonacci spirals, it's solving a complex packaging problem.
If the sunflower seeds arranged any other way, they would leave gaps or create crowding. The Fibonacci solution maximizes the number of seeds while ensuring each one gets adequate space, light, and protection.
The same principle applies to leaf arrangement. Plants that position their leaves according to Fibonacci ensure that each leaf gets maximum sunlight exposure without being shaded by the ones above it. It's not that plants "know" about Fibonacci numbers—it's that plants with these arrangements outcompete those without them.
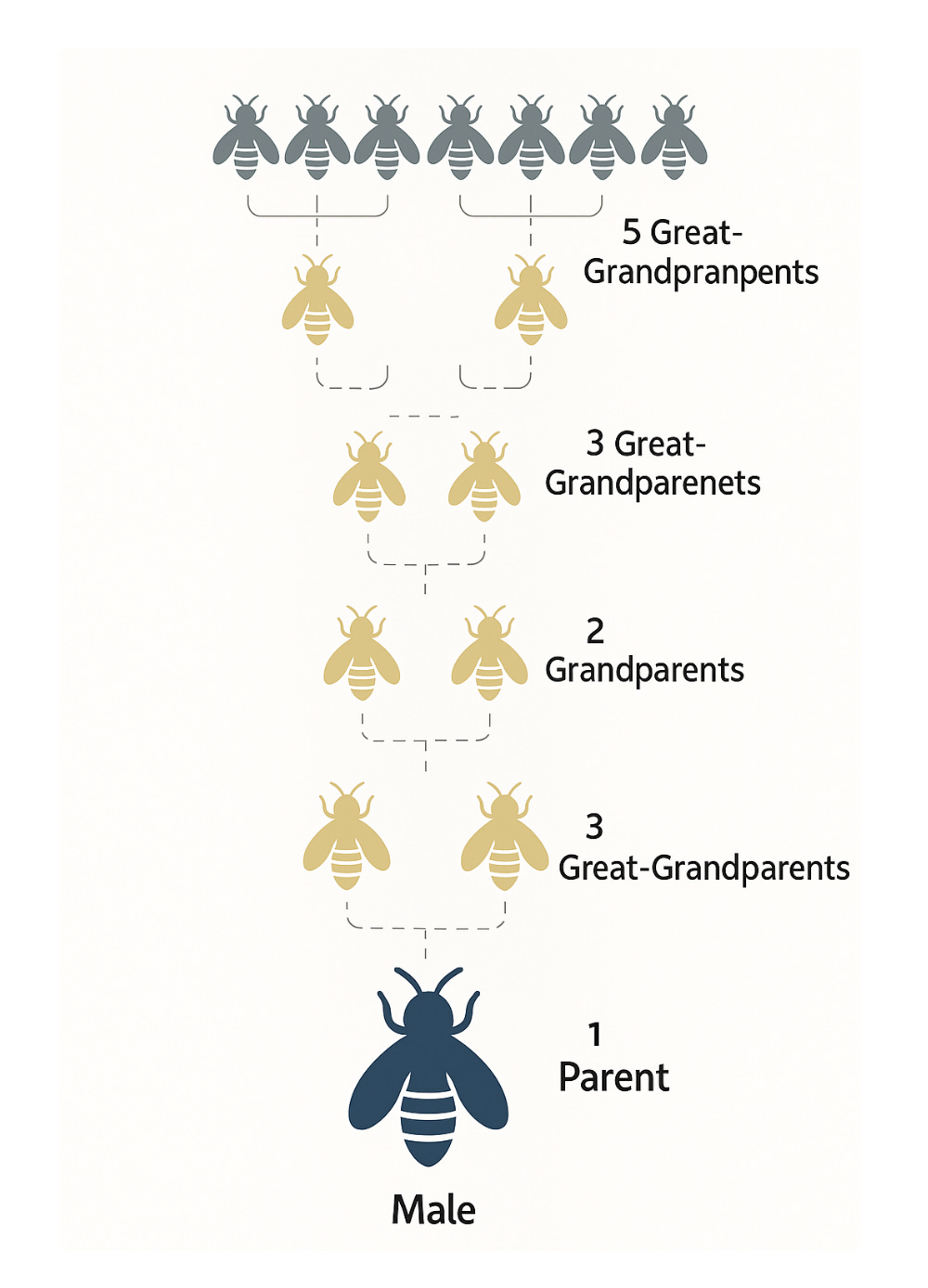
In animals, the story is more complex but equally fascinating. The genealogy of male honeybees forms a perfect Fibonacci tree because of their unusual reproductive system. A male bee has only one parent (the queen), but two grandparents, three great-grandparents, and so on, following the Fibonacci sequence exactly.
The nautilus shell, often cited as a perfect example of the Golden Spiral, is actually more complex. While its spiral does approximate the Golden Spiral, it's not exact—the nautilus has evolved its own optimization based on the physics of shell growth and structural integrity.
The Human Body: Measuring Ourselves Against Mathematics
Claims about φ in human anatomy are among the most controversial applications of the Golden Ratio. Some assert that the ratio of your height to the distance from your navel to the floor equals φ, or that your face reflects Golden Ratio proportions in various measurements. The idea of a universal "Golden Ratio human" is more myth than reality, a testament to our desire to find perfect order even in our messy biological selves.
And yet, traces of φ do appear in subtler ways. Certain facial proportions—the length of the face compared to its width, the spacing of the eyes, the balance between nose, lips, and chin—often fall close to the Golden Ratio. Dr. Stephen Marquardt even created a “Golden Mask” based on these ratios, and across cultures, people consistently rate faces that align with it as more attractive. We don’t consciously measure these proportions, but our eyes seem tuned to them. A face built on φ feels harmonious in the same way a perfectly balanced chord resonates in music.
Fibonacci’s sequence also leaves its imprint on us. The relative lengths of finger bones follow it, each segment approximating the sum of the two before it. Ratios between facial features often echo Fibonacci numbers as well, converging toward φ. Just as sunflowers pack their seeds according to Fibonacci spirals, the human body carries echoes of the same growth logic. Perhaps our sense of beauty is sharpened by lifelong exposure to these patterns in nature—so when we encounter them in another person, they feel at once familiar and compelling.
But beauty resists being reduced to a single formula. Lucas numbers, Fibonacci’s mathematical cousins, provide another pathway to φ. They converge on the same Golden Ratio from different starting points, introducing variation into the harmonies of proportion. This may help explain why different cultures and individuals celebrate slightly different ideals of beauty. Too much symmetry or too rigid an adherence to φ can look artificial. Lucas-like deviations create uniqueness, which our perception interprets as vitality.
Taken together, these patterns suggest that beauty emerges from a dialogue between universal structure and individual variation. The Golden Ratio provides the skeleton of balance and harmony. Fibonacci sequences layer in the rhythms of natural growth. Lucas numbers remind us that deviation is not error but expression. We are pattern-seeking creatures, and in the play between these mathematical truths and the uniqueness of each human form, we find the faces and bodies that move us.
The DNA double helix provides an even more concrete example of this hidden geometry: it measures 34 angstroms long and 21 angstroms wide per complete cycle—two consecutive Fibonacci numbers whose ratio approximates φ. Here, at life’s most fundamental level, mathematics is not just metaphor but structure, suggesting that harmony and proportion are woven into our very biology, not as a conscious design choice but as an emergent property of how complex molecules optimize their structure in three-dimensional space.
Spirals in Space and Time
Scale up from molecules to galaxies, and the patterns persist. Hurricane formations follow spiral patterns that approximate the Golden Spiral, not because they're trying to be beautiful but because this shape represents the most efficient way for energy to dissipate in a rotating system.
Galaxy arms spiral in similar patterns, shaped by the interplay of gravity, rotation, and conservation of angular momentum. Ocean waves curl in Golden Spirals as they break. Even the cochlea in your inner ear—the organ that allows you to hear—is shaped like a spiral that follows φ proportions, optimized to distinguish between different frequencies of sound.
The Blueprint for Progress: Using This Knowledge for Good
Now that we've glimpsed these hidden blueprints, a more pressing question emerges: how can we use this profound understanding of the universe's quiet architecture to better our world? This isn't just an exercise in intellectual curiosity; it's a foundation for human progress.
Biotechnology and medicine: understanding these fundamental patterns could revolutionize drug delivery and material science. We might design more efficient biomimetic materials—synthetic bone structures or drug-releasing polymers—by mimicking the mathematical principles that govern natural growth and efficiency. By applying the optimization rules of the Golden Ratio to create medical implants, we could ensure they integrate seamlessly with human tissue, which itself adheres to similar mathematical logic.
Environmental sustainability: this knowledge is crucial for creating more resilient and efficient systems. Imagine designing solar panel arrays that, like a sunflower's head, maximize light absorption by using a Fibonacci-based layout. Or consider urban planning that uses Golden Spiral principles to design more efficient public transportation networks or to ensure that parks and green spaces are geometrically optimized for human and ecological well-being.
Space exploration and technology: these principles have already proven their worth. As the Kolmogorov-Arnold-Moser theorem suggests, a deeper understanding of orbital dynamics tied to irrational numbers like φ can help us design more stable and long-lasting satellites and probes. We could model the stable orbits of future space colonies or design self-sustaining ecosystems that use Fibonacci-like growth patterns to optimize resource use. As the late astronomer and author Carl Sagan once mused, "The nitrogen in our DNA, the calcium in our teeth, the iron in our blood, the carbon in our apple pies were made in the interiors of collapsing stars. We are made of star stuff." We might now add that the very structure of that "star stuff" follows a beautiful, universal mathematical code.
The discovery of the Golden Ratio's presence in the cosmos is more than a beautiful coincidence. It's an invitation to think differently, to recognize that the most elegant solutions to our problems may not be brute force but rather reflections of the same elegant principles that govern a spiraling galaxy and a single seashell. We are not just observers of this mathematical reality; we are participants, bystanders, and by learning its language, we can perhaps shape a future that is as efficient and harmonious as the universe itself.




Hey Bill,
Question - To what extent do the appearances of φ in nature represent true "causal relationships" versus patterns identified by human perception AFTER the fact (IE, correlation versus causation)??
love this!! do you think you could recommend me some good books to read about the Fibonacci sequence? I'm a relatively beginner reader so I can't have a book too in depth just yet but I'm so fascinated and I want to learn more about why the sequence is so amazing!